
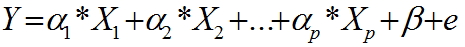
Using the same approach, you will obtain the value #N/A from the resulting formula of form =LinEqSolve(R1). Where u and v are any (complex) constants.Įxample 3: Solve the following system of linear equations There are an infinite number of solutions all of the form The approach is similar to that used for Example 1. Examples with non-unique solutionsĮxample 2: Solve AX = C with A = the matrix in range B3:D4 and C = the vector in range E3:E4 of Figure 2. This is accomplished using the worksheet formula =ZMROUND(ZText(ZSet(O7:O9,O10:O12)),4). We can then represent this solution vector in Excel format as shown in range Q7:Q9 with the entries rounded off to 4 decimal places. The resulting solution to the real linear equations in G7:M12 is shown in range O7:O12 using the formula =LinEqSolve(G7:M12). We next reformat this augmented matrix to the format required by Property 1, as shown in range G7:M12. The same matrix in Real Statistics format is shown in range G3:N5, using the formula =ZMap(B3:E5).įigure 1 – Unique Solution to Complex Linear Equations The augmented matrix in Excel format is shown in range B3:E5 of Figure 1. Example with unique solutionĮxample 1: Solve the following linear equations. Then X-tilde is a solution to the real-valued linear equations is equivalent to X = X r + X ci is a solution to the original system of linear equations AX = C. We now consider the following set of 2 n real-valued linear equations in 2 n unknowns Similarly, any complex matrix Z can be represented as Furthermore, we can represent any complex number z as Now suppose that A and C can have complex entries, and so the solution vector X can also have complex entries. As we have seen in Systems of Linear Equations, we can represent this in matrix form as Suppose we have a set of n linear equations in n unknowns.


 0 kommentar(er)
0 kommentar(er)
